Die Kraft von XOR: Dekodieren des exklusiven oder Tors

Das XOR-Gate (exklusiv-or) ist ein wichtiges Instrument in der digitalen Elektronik und spielt eine Schlüsselrolle beim Entwerfen von Schaltungen.Dieses spezielle Tor macht mehr als grundlegende Aktionen wie und, oder und nicht.Es folgt einer einfachen, aber wichtigen Regel: Es gibt nur eine echte Ausgabe, wenn nur einer seiner Eingänge wahr ist.Dies unterscheidet es sich von anderen Logikstoren und nützlich in komplexen digitalen Systemen.In diesem Artikel wird untersucht, wie das Xor Gate funktioniert, von seinem grundlegenden Setup mit Transistoren bis hin zu seinen verschiedenen Designs, die NAND und NOR -Gates verwenden, um den wichtigen Platz in der modernen Elektronik besser zu verstehen.

Katalog

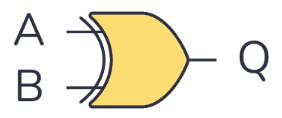
Das Xor -Tor verstehen

Das XOR (exklusive oder) Gate spielt eine Hauptaufgabe in digitalen Schaltkreisen und bietet eine Funktion, die sich von grundlegenden booleschen Operationen wie OR, und, und nicht, unterscheidet.Im Gegensatz zum oder dem Gate, das den Booleschen Addition oder das und Gate als Multiplikation ausführt, folgt der XOR einer anderen Regel.Es gibt aus wahr (1) nur, wenn genau einer seiner Eingänge wahr ist, machen es zu einer einzigartigen und wertvollen Komponente im Logikdesign.

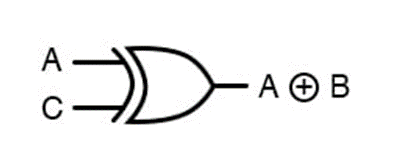
Abbildung 2. XOR Gate

In Schaltplätzen und Logikdiagrammen wird das XOR durch ein bestimmtes Symbol dargestellt.Es ist jedoch nicht so häufig in den Booleschen algebraischen Vereinfachungen enthalten, da viele boolesche Standardeigenschaften - wie verteilende, assoziative und kommutative Gesetze - nicht direkt für XOR -Operationen gelten.

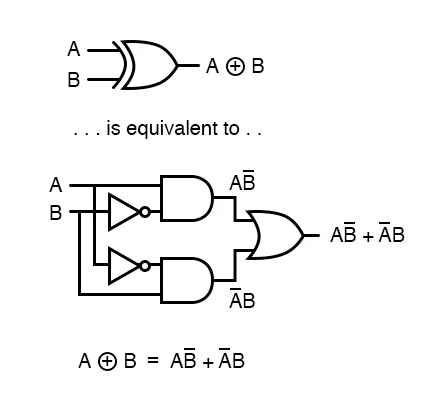
Abbildung 3. Die exklusive oder und und und und und und und und und und und Sie

Trotzdem kann ein XOR immer noch mit anderen Grundtoren ausgedrückt werden: Ab ' + a'b.Diese Formel ist mehr als ein fiktives Konstrukt;Es hat praktische Vorteile bei der Schaltungsdesign.Das Ersetzen mehrerer logischer Operationen durch ein einzelnes XOR -Gate vereinfacht Schaltungslayouts, verringert die Komplexität und die Verbesserung der Effizienz.Diese Optimierung ist in fortschrittlichen digitalen Systemen größtenteils vorteilhaft, wobei die Minimierung unnötiger Komponenten zu einer besseren Leistung und einem geringeren Stromverbrauch führt.

Implementierung eines XOR -Gate mit Transistoren

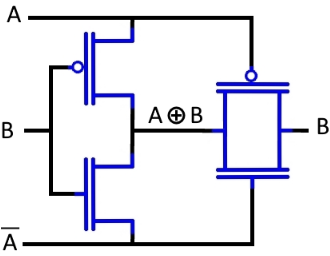
Abbildung 4. XOR -Tor mit Transistoren

Der Aufbau eines XOR -Gates mit Transistoren zeigt das sorgfältige Design, das in digitalen Schaltungen erforderlich ist.Dieses Setup stellt sicher, dass die Schaltung korrekt auf alle möglichen Eingangskombinationen reagiert.Für ein XOR-Gate mit zwei Eingängen sind mehrere Transistoren erforderlich, die vier Szenarien verarbeiten: Beide Eingänge niedrig (0,0), ein Eingang hoch und der andere niedrig (1,0 oder 0,1) und beide Eingänge hoch (1,1).Jede Bedingung aktiviert oder deaktiviert spezifische Transistoren, steuert den Stromfluss und die Bestimmung des Ausgangs.

Wann Beide Eingänge sind niedrig (0,0)Die mit diesen Eingaben verbundenen Transistoren bleiben ausgeschaltet und verhindern, dass jeder Strom den Ausgang erreicht.Infolgedessen bleibt die Schaltung offen und der Ausgang bleibt niedrig (0).Wenn Ein Eingang ist hoch, während der andere niedrig ist (1,0 oder 0,1), ein spezifischer Transistorpfad schließt sich, wodurch der Strom zum Ausgang fließen kann.Diese Aktivierung erzeugt einen hohen Ausgang (1), der verwendet werden kann, um eine LED einzuschalten oder eine andere Komponente auszulösen.Allerdings wann Beide Eingänge sind hoch (1,1), ein zusätzlicher Transistorensatz leitet den Strom vom Ausgang weg und zwingt ihn wieder in einen niedrigen Zustand (0).Dieses Verhalten folgt der XOR -Regel: Die Ausgabe ist nur hoch, wenn die Eingänge unterschiedlich sind und niedrig bleiben, wenn sie gleich sind.

Dieses auftransistorbasierte XOR-Gate bietet eine klare, praktische Demonstration, wie digitale Schaltkreise Prozesslogik verarbeiten.Durch die Steuerung elektrischer Wege basierend auf Eingangsbedingungen veranschaulicht die Schaltung die Kernprinzipien der Booleschen Logik in Aktion.Dieses Design ist nicht nur fiktiv, sondern dient als ursprüngliches Konzept für das Verständnis komplexerer digitaler Systeme.

Konfigurieren eines XOR -Gate mit nur NAND -Toren

Abbildung 5. XOR Gate mit nur NAND -Toren

Das Erstellen eines XOR -Gates mit nur NAND -Gates zeigt die Flexibilität und endgültige Bedeutung der NAND -Logik im Schaltungsdesign.Da wird Xor normalerweise als ausgedrückt als A'b + ab 'Es kann mit nur NAND -Gates durch Bewerbung neu geschrieben werden De Morgans Gesetze und das Prinzip der doppelten Negation.

Der Prozess beginnt mit der Negation jeder Eingabe mit einem einfachen NAND -Betrieb.Dies bedeutet, A und B in separate NAND -Gates zu füttern, bei denen jeder Eingang mit sich selbst gepaart wird und produziert wird A 'und B'.Diese negierten Werte werden dann in zusätzlichen Nand -Gate -Stadien verwendet, um den Ausdruck zu bilden (A'.b) ’.(A.b) ’, was letztendlich wieder zur Standard -XOR -Formel vereinfacht, A'b + ab '.

Diese Methode zeigt, wie NAND -Gates jede logische Funktion, einschließlich XOR, replizieren kann, indem mehrere Stufen auf strukturierte Weise kaskadiert.Während diese Konfiguration mehr Gates als ein dediziertes XOR -Gate erfordert, verstärkt sie ein Hauptkonzept in der digitalen Logik: Das NAND -Tor allein reicht aus, um eine Logikschaltung zu erstellen.Das Verständnis dieses Prinzips hilft Ihnen, zu erkennen, wie grundlegende Bausteine ​​angeordnet werden können, um komplexe Vorgänge durchzuführen, eine wichtige Fähigkeit im Digital Circuit Design.

Konstruktion eines XOR -Gate

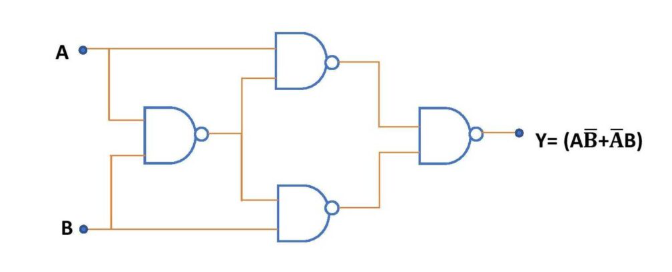
Abbildung 6. Konstruktion eines XOR -Gate

Ein XOR -Gate kann nur mit Gates erstellt werden, wodurch die Anpassungsfähigkeit grundlegender Logikkomponenten im Digital Circuit -Design demonstriert wird.Dieser Ansatz erfordert mehrere Stufen, wobei jeder Schritt die logischen Signale sorgfältig formt, um die richtige XOR -Ausgabe zu erzeugen.

• Der Prozess beginnt damit, beide Eingänge in ein Nor -Gate zu füttern, das eine Ausgabe erzeugt, die die Umkehrung ihrer Summe ist.Dies bedeutet, dass, wenn eine Eingabe hoch ist (1), der Nor Gate niedrig (0).Wenn beide Eingänge niedrig sind (0), ist der Ausgang hoch (1).

• Als nächstes werden die ursprünglichen Eingänge und die invertierte Summe in zwei separaten Toren verwendet.Jedes dieser Tore erhält eine der ursprünglichen Eingänge zusammen mit der zuvor umgekehrten Summe.Diese Zwischenstufen verfeinern die logischen Signale und stellen sicher, dass die Schaltung korrekt zwischen verschiedenen Eingangsbedingungen unterscheidet.

• Schließlich werden die Ausgänge dieser beiden Zwischen- und Tore in ein viertes oder ein Tor versetzt.Diese letzte Stufe dreht die kombinierten Ergebnisse um und erzeugt die endgültige XOR -Ausgabe.Die XOR -Funktion ist jetzt vollständig realisiert, wobei der Ausgang hoch (1) nur dann ist, wenn die Eingänge unterschiedlich und niedrig sind (0), wenn sie gleich sind.

Dieses NOT-basierte XOR-Gate unterstreicht die Fähigkeit, komplexe Logikoperationen mit nur einer einzigen Gate-Art zu konstruieren.Das Verständnis dieses Ansatzes ist im digitalen Design wertvoll, da NOR -Gates - wie NAND -Gates - funktionell vollständig sind, was bedeutet, dass sie kombiniert werden können, um eine logische Funktion zu erstellen.Diese Methode ist meist nützlich bei Anwendungen wie Fehlererkennung und Korrektur, bei denen XOR -Operationen eine wichtige Rolle bei der Überprüfung der Datenintegrität spielen.

XOR-Gate mit drei Eingängen

Abbildung 7. XOR-Gate mit drei Eingängen

Das Hinzufügen eines dritten Eingangs zu einem XOR -Gate erhöht seine Komplexität und erweitert seine Nützlichkeit im Digital Circuit Design.Ein XOR-Gate mit drei Eingaben erzeugt nur dann einen hohen Ausgang (1), wenn eine ungerade Anzahl seiner Eingänge hoch ist.Diese Regel erstreckt sich auf natürliche Weise auf XOR-Gates mit mehr Eingaben, sodass sie in Logiksystemen mit mehreren Eingängen wertvoll sind.

Um zu verstehen, wie dieses Tor arbeitet, berücksichtigen Sie seine Wahrheitstabelle, die alle möglichen Eingabekombinationen beschreibt.Wenn die Anzahl der hohen Eingänge ungerade (1 oder 3) ist, ist der Ausgang hoch (1).Wenn die Anzahl der hohen Eingänge gleichmäßig ist (0 oder 2), bleibt die Ausgabe niedrig (0).Dieses Verhalten macht XOR-Gates mit drei Eingängen besonders nützlich bei der Paritätsprüfung und bei der Erkennung von Fehler, wobei sichergestellt wird, dass die Datenintegrität von der Erkennung von Bit-Flip-Fehlern abhängt.

Ein XOR-Gate mit drei Eingängen kann mit Basic und, oder und nicht mit Toren oder ausschließlich mit NAND oder NOR-Toren erstellt werden.Diese alternativen Implementierungen zeigen die Anpassungsfähigkeit des XOR GATE und zeigen, wie sie aus verschiedenen Logikkomponenten konstruiert werden können und gleichzeitig seine Kernfunktion erhalten.Diese Flexibilität wird in fortschrittlichen Schaltungskonstruktionen verwendet, bei denen die Minimierung von Gate -Typen oder die Optimierung bestimmter Hardwarebeschränkungen erforderlich ist.Durch effektives Verwalten mehrerer Eingaben spielt das XOR -Gate eine ultimative Rolle bei der Schaffung effizienter und zuverlässiger digitaler Systeme.

Verwendung des XOR -Tores

Das XOR -Gate spielt aufgrund seines einzigartigen logischen Verhaltens eine ernsthafte Rolle in verschiedenen digitalen Anwendungen.

Datenverschlüsselung

Eine seiner wichtigsten Verwendungen ist die Datenverschlüsselung, bei der Datenbits mit Schlüsselbits kombiniert werden, um Informationen zu verdecken, was es für nicht autorisierte Parteien schwer macht, zugreifen zu können.Diese grundlegende Technik, die als bitweise XOR -Verschlüsselung bezeichnet wird, wird in kryptografischen Algorithmen häufig verwendet, um empfindliche Daten zu sichern.

Digitale Schaltungen

In digitalen Schaltungen sind XOR -Gates für Vergleiche nützlich, die überprüfen, ob zwei binäre Werte gleich sind.Sie werden auch in arithmetischen Operationen verwendet, wo sie dazu beitragen, Summen zu berechnen und Carry -Signale in Adierern und Subtrahieren zu verwalten.Durch effizientes Umgang mit Binärberechnungen verbessern XOR Gates die Genauigkeit und Leistung dieser Prozesse.

Speicherspeicher und Adressdecodierung

Über die Arithmetik hinaus werden XOR -Gates in Speicherspeichersystemen und der Adressdecodierung häufig verwendet, wobei sie dazu beitragen, den Datenfluss und die Zugriffskontrolle zu verwalten.Sie tragen auch zur Zufallszahlengenerierung bei, was für Simulationen, Kryptographie und sichere Kommunikation wichtig ist.

T Flip-Flops

XOR-Gates spielen eine Schlüsselrolle in T-Flip-Flops, wo sie den Zustand der Umschaltung auf Taktimpulse ermöglichen.Diese Funktion ist nützlich für das Timing und die Synchronisation in sequentiellen Schaltungen, um sicherzustellen, dass digitale Systeme reibungslos und zuverlässig funktionieren.

Vor- und Nachteile von Xor Gates

Vorteile von Xor Gates

XOR -Gates werden in digitalen Schaltungen benötigt, hauptsächlich für Fehlererkennung und Paritätsprüfung.Sie sollen feststellen, ob eine Die ungerade Anzahl von Eingängen ist hoch (1), eine Schlüsselfunktion in Systemen, die die Datenintegrität gewährleisten.Diese Eigenschaft macht Xor Gates ultimativ in beiden einfache und komplexe logische Operationen, sodass sie Berechnungen rationalisieren und die Schaltungseffizienz verbessern können.

Ein weiterer großer Vorteil von Xor Gates ist ihre Fähigkeit, komplexe logische Funktionen mit relativ wenigen Komponenten auszuführen.Diese Effizienz verringert die Anzahl der erforderlichen Logik -Gates in einigen Designs, macht Schaltkreise kompakter und verbessert die Gesamtleistung.Ihre Vielseitigkeit erstreckt sich auch auf arithmetische Operationen, Verschlüsselung und SignalverarbeitungVerstärkung ihrer Rolle in einer Vielzahl von Anwendungen.

Nachteile von Xor Gates

Trotz ihrer Nützlichkeit haben Xor Gates einige Nachteile.Wenn Schaltungen weiter fortgeschritten werden, Das Implementieren von XOR -Funktionen mit mehreren Eingaben erhöht die Konstruktionskomplexität.Weitere Eingaben erfordern zusätzliche Tore, was zu höherer Stromverbrauch und längere Ausbreitungsverzögerungen.Diese Faktoren können sich negativ auf die Geschwindigkeit und Effizienz digitaler Systeme auswirken, insbesondere in zeitempfindlichen Anwendungen.

Darüber hinaus kann die Fehlerbehebung und Aufrechterhaltung von Schaltkreisen, die stark auf Xor Gates angewiesen sind, eine Herausforderung sein.Wenn die Anzahl der Eingänge wächst, wird die Logikstruktur komplizierter, was sie macht schwerer zu diagnostizieren und die Leistung zu optimieren.Sie müssen sorgfältig Gleiche die Vorteile von Xor Gates mit ihren potenziellen NachteilenSicherstellung effizienter Schaltungskonstruktionen, die die Komplexität minimieren und gleichzeitig die Zuverlässigkeit maximieren.

Abschluss

Das XOR -Gate ist ein Schlüsselstück im Digital Circuit Design, das für seine einzigartige Art der Verarbeitung von Signalen bekannt ist.Es ist gut darin, verschiedene Aufgaben zu erledigen, von Erkennen von Fehlern bis hin zum Verschlüsseln von Daten, was es in vielen Anwendungen sehr wichtig macht.Obwohl es einige Herausforderungen und Nachteile gibt, XOR Gates in komplexen Schaltungen zu verwenden, sind ihre Vorteile, wie die Anzahl der benötigten Teile und die Steigerung der Leistung, klar.Während die digitale Technologie weiter voranschreitet, spielt das XOR -Gate weiterhin eine dynamische Rolle und stellt sicher, dass die Systeme gut funktionieren und für zukünftige Verbesserungen bereit sind.Dieser tiefe Tauchgang zeigt, dass das XOR -Tor mehr als nur ein Teil der digitalen Logik ist.Es ist ein wichtiges Element, das den Datenfluss in unserer digitalen Welt verwaltet.

Häufig gestellte Fragen [FAQ]

1. Warum wird das XOR -Tor als exklusives oder Tor bezeichnet?

Das XOR -Gate wird als "exklusiv oder" bezeichnet, da es nur dann true oder 1 ausgibt, wenn die Eingänge ausschließlich das eine oder andere, aber nicht beide sind.Diese Exklusivität - wo nur ein Eingangszustand zu einer hohen Ausgabe führt, während gemeinsame Eingangszustände (sowohl wahr oder beides False) zu einer niedrigen Ausgabe führen - unterscheidet sie vom Standard oder Gate, das True ausgibt, wenn einer oder beide Eingänge wahr sind.

2. Was ist der boolesche Ausdruck für das exklusive oder XOR -Tor?

Der boolesche Ausdruck für ein XOR -Gate ist A⊕b, das auf (a∧b) ∨ (¬a∧b) erweitert werden kann.Dies bedeutet, dass die Ausgabe wahr ist, wenn entweder A oder B wahr ist, aber nicht beides.

3. Was ist der Ausdruck des XOR -Tores?

Der Ausdruck für das XOR -Gate ähnelt dem mit Booleschen Ausdruck bereitgestellten Ausdruck.Es kann als A⊕B dargestellt werden, was zu A · B + Aëb vereinfacht wird.Dies spiegelt die Betriebsregel wider, bei der die Ausgabe nur dann hoch ist, wenn sich die Eingaben unterscheiden.

4. Was ist das Prinzip des XOR?

Das Prinzip des XOR -Tors besteht darin, zwei Eingangssignale zu vergleichen und eine Ausgabe zu liefern, die nur dann zutrifft, wenn sich die Eingänge voneinander unterscheiden.In praktischen Szenarien, wie z. B. in digitalen Schaltungen zur Fehlererkennung, hilft das XOR -Gate bei der Identifizierung von Diskrepanzen, da es wie ein Differenzdetektor wirkt, und nur die Signalisierung, wenn Eingänge nicht ausgerichtet sind.

5. Wie ist die Beziehung zwischen Xor und oder?

Die Beziehung zwischen XOR und oder Gates liegt in ihrem Ausgangsverhalten als Reaktion auf binäre Eingänge.Während das oder Gate TRUE ausgibt, wenn mindestens eine der Eingänge wahr ist, benötigt das XOR -Gate genau einen Eingang, um für eine echte Ausgabe wahr zu sein.Der XOR kann als selektivere Version des oder Gate angesehen werden, was der grundlegenden Inklusivität der oder Funktion einen Zustand der Exklusivität hinzufügt.