Die vollständige Anleitung zu RC -Schaltungen und Zeitkonstanten

RC -Schaltkreise sind grundlegende Bausteine ​​in der Elektronik, die zum Timing, Filterung und Signalformung verwendet werden.Durch die Kombination eines Widerstandes und eines Kondensators in Reihe sind diese Schaltungen steuern, wie sich Spannung und Strom im Laufe der Zeit verhalten, insbesondere bei Übergängen wie Ladung oder Entlassung.Dies zu diesem Verhalten zu führen ist die Zeitkonstante (T = R × c), was bestimmt, wie schnell oder verlangsam diese Änderungen auftreten.In diesem Artikel wird die Kernprinzipien hinter RC -Schaltkreisen aufgeschlüsselt, die Mathematik in praktischer Hinsicht erläutert und zeigt, wie tatsächliche Anwendungen mit dem RC -Timing entworfen, simulieren und analysiert werden.

Katalog

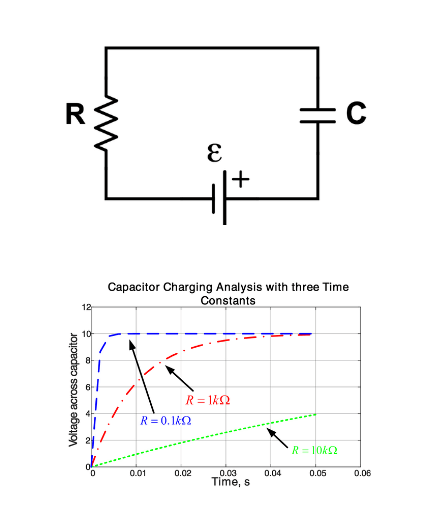
RC -Schaltungsverhalten und Zeitkonstante

Eine RC -Schaltung besteht aus einem Widerstand (R) und einem Kondensator (c), der in Reihe mit einer Stromquelle angeschlossen ist.Wenn die Schaltung aktiviert ist, beginnt der Kondensator durch den Widerstand zu laden.Der Widerstand verlangsamt sich, wie schnell die Ladung aufbaut.Wenn die Spannung des Kondensators steigt, fällt der Spannungsabfall über den Widerstand.Diese Wechselwirkung ist nach der Zeitkonstante geformt, T, was dem Produkt von Widerstand und Kapazität entspricht (KapazitätT = R × c).Es bestimmt, wie schnell oder verlangsam die Kondensatorladungen.

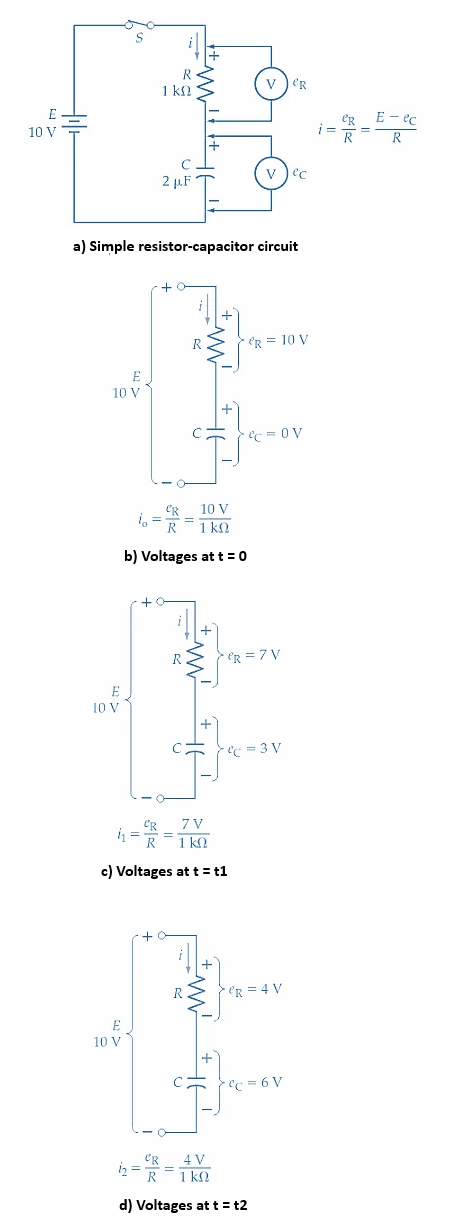
Abbildung 2. Kondensatorspannung in einer Serien -CR -Schaltung

Zu Beginn (in Abbildung 1a) hat der Kondensator keine gespeicherte Spannung.In dem Moment, in dem der Schalter geschlossen ist, fällt die vollen 10 Volt der Stromquelle über den Widerstand ab.Ohne Spannung auf dem Kondensator liegt der Anfangsstrom am höchsten Wert:

i₀ = (10 V - 0 V) ​​/ 1 kΩ = 10 mA

Mit der Zeit baut der Kondensator Spannung auf.Zu einem späteren Punkt (t = t₁) erreicht der Kondensator 3 Volt.Dadurch bleibt 7 Volt über den Widerstand.Aufgrund der reduzierten Spannungsdifferenz fällt auch der Strom ab:

i₁ = (10 V - 3 V) / 1 kΩ = 7 mA

Weiter in der Zeit (t = T₂) hat der Kondensator 6 Volt erreicht.Das bedeutet, dass nur 4 Volt über den Widerstand gelassen werden, und der Strom fällt noch mehr ab:

i₂ = (10 V - 6 V) / 1 kω = 4 mA

Jedes Mal, wenn der Kondensator mehr Spannung erhält, nimmt der Strom ab.Dies bedeutet, dass der Ladevorgang im Laufe der Zeit verlangsamt.Die Spannungserhöhung erfolgt nicht mit einer konstanten Geschwindigkeit. Es folgt einer exponentiellen Kurve, wie in Abbildung 2 dargestellt. Mit anderen Worten, es dauert länger und länger, um jeden zusätzlichen Volt zu gewinnen.

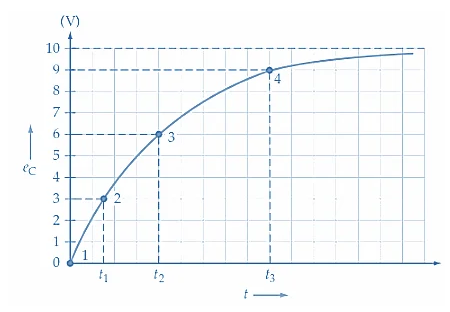
Abbildung 3.. Typisches Wachstum der Kondensatorspannung im Vergleich zur Zeit für eine Serie RC -Schaltung

Schließlich wird die Spannung des Kondensators nahezu der Versorgungsspannung.Zu diesem Zeitpunkt wird der Stromfluss fast Null.Der Stromkreis setzt sich in einen stetigen Zustand ein, bei dem keine merklichen Änderungen mehr auftreten.Dieser vollständige Übergang von der anfänglichen Stromsteigung bis zur allmählichen Auswertung ist bekannt als die Schrittantwort oder erzwungene Antwort einer RC -Schaltung.

Sofortspannung und Strom in einem RC -Schaltkreis

Spannung über einen Ladekondensator

Wenn ein Kondensator durch einen Widerstand an eine Spannungsquelle angeschlossen ist, nimmt seine Spannung im Laufe der Zeit in einem spezifischen Muster zu, das durch eine exponentielle Funktion beschrieben wird.Dieses Wachstum ist nicht linear, verlangsamt sich jedoch, wenn der Kondensator berechnet.

Die Spannung über den Kondensator wird jederzeit mit der Formel berechnet:

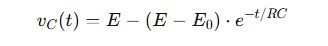
Wo:

• v_C(T) ist die Spannung über den Kondensator zum Zeitpunkt t (in Sekunden).

• E ist die endgültige oder Versorgungsspannung (in Volt).

• E_₀ ist die Anfangsspannung des Kondensators bei T = 0.

• R ist der Widerstand in Ohm (ω).

• C ist die Kapazität in Farads (f).

• e ist Euler -Nummer, ungefähr 2,718.

Vereinfachter Fall: Anfänglich nicht aufgeladener Kondensator

Wenn der Kondensator von Null Volt (e) beginnt_₀ = 0), die Gleichung wird:

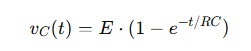
Diese vereinfachte Form wird üblicherweise bei der Analyse von Schaltungen verwendet, bei denen der Kondensator vollständig entlassen wird.

Finden der Ladezeit für eine bestimmte Spannung

Um festzustellen, wie lange es dauert, bis der Kondensator einen bestimmten Spannungs -VC erreicht hat, ordnen wir die Gleichung neu an:

Dieser Ausdruck bietet eine Möglichkeit, die Zeit t auf dem gewünschten Spannungsniveau zu finden.

Beispiel 1: Zeit bis zur Erreichung gegebener Spannungen

Betrachten Sie eine Schaltung mit den folgenden Werten:

• Widerstand r = 1 kΩ

• Kapazität C = 2 μF

• Versorgungsspannung e = 10 V

Berechnen Sie nun die Zeit, die erforderlich ist, um bestimmte Spannungen zu erreichen:

Für 3 V:

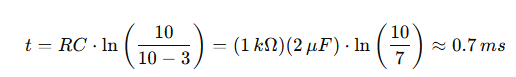
Für 6 V:

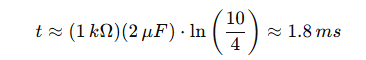
Für 9 V:

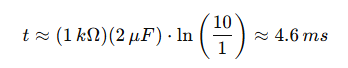
Beispiel 2: Spannung erhöht sich im Laufe der Zeit

Diese Tabelle zeigt, wie die Kondensatorspannung in regelmäßigen Abständen zunimmt:

Zeit (t)	Kondensator Spannung (Eₙ)	Aufzeigen Abbildung 4
Bei t = 0	eₙ = 0	Punkt 1
Bei t = 1 ms	EC = 10 V (1 - E - 1MS/2 μF × 1KΩ) = 3,93 V	Punkt 2
Bei t = 2 ms	Eₙ ≈ 6,32 V	Punkt 3
Bei t = 3 ms	Eₙ ≈ 7,77 V	Punkt 4
Bei t = 4 ms	Eₙ ≈ 8,65 V	Punkt 5
Bei t = 5 ms	eₙ ≈ 9.18 V	Punkt 6
Bei t = 6 ms	Eₙ ≈ 9,5 V	Punkt 7
Bei t = 7 ms	Eₙ ≈ 9,7 V	Punkt 8
Bei t = 8 ms	Eₙ ≈ 9,82 V	Punkt 9
Bei t = 10 ms	Eₙ ≈ 9,93 V	Punkt 10
Bei t = ∞	Eₙ ≈ 10 V (maximaler Spannungsniveau)	-

Diese Daten zeigen, dass die Spannung etwa 63,2% der Versorgungsspannung bei erreicht T = RC = 2 ms.Von T = 5RC = 10 ms, der Kondensator ist über 99,3% aufgeladen.

Zeitkonstante

Die Zeitkonstante (gekennzeichnet durch den griechischen Brief Toder Tau) ist ein wesentliches Maß dafür, wie schnell ein Kondensatorgebühren oder Ableitungen berechnet werden.Es ist definiert als:

T = RC

Folgendes sagt es uns:

• Nach einmal konstant (T = RC)Der Kondensator hat etwa 63,2% der Versorgungsspannung berechnet.

• Nach fünf Zeitkonstanten (T = 5RC)Es hat mehr als 99%berechnet.

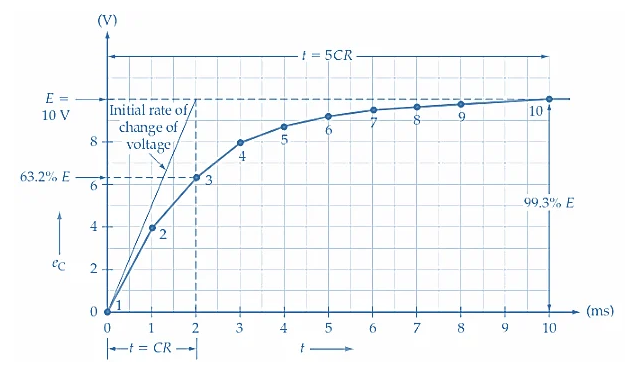
Abbildung 4. Diagramm der Kondensatorspannung

Im Laufe der Zeit berechnet der Kondensator langsamer.Dies liegt daran, dass der Spannungsunterschied zwischen der Versorgung und dem Kondensator abnimmt und den Strom verringert.Obwohl der Kondensator niemals mathematisch 100% der Versorgungsspannung erreicht, kommt er nach mehreren Zeitkonstanten extrem eng.

Strömungsstrom und sein Verhalten

Wenn der Kondensator berechnet, ändert sich auch der Strom, der in ihn fließt.Es beginnt hoch und nimmt allmählich ab.Der Ausdruck für den Strom ist zu irgendeinem Zeitpunkt t:

Diese Formel zeigt, dass der Ladestrom einem exponentiellen Zerfall folgt.

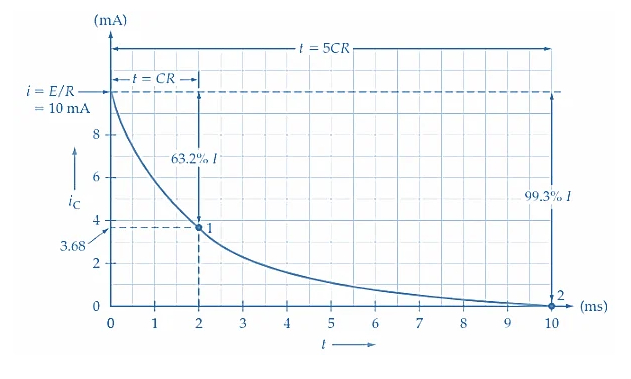
Abbildung 5. Kondensatorladestrom

Zu Beginn befindet sich die volle Versorgungsspannung über den Widerstand, so dass der Strom am höchsten ist.Wenn der Kondensator berechnet, steigt die Spannung über sie und verringert die Spannung über den Widerstand, was wiederum den Strom senkt.Schließlich wird der Strom vernachlässigbar, wenn sich die Spannung über den Kondensator dem Versorgungsniveau nähert.

Berechnung der Zeitkonstante (T) in einem RC -Schaltkreis

In einer RC -Schaltung die Zeitkonstante, geschrieben als T (Tau)Erzählt Ihnen, wie schnell der Kondensator berechnet oder entlassen wird.Es ist ein grundlegendes, aber wichtiges Konzept in der Schaltungsdesign, insbesondere wenn das Timing -Verhalten von Bedeutung ist.

Die Formel ist einfach:

T = R × c

Wo:

• R ist der Widerstand in Ohm (ω)

• C ist die Kapazität in Faraden (f)

• T ist die Zeitkonstante, gemessen in Sekunden

Wie man berechnet T?

• Finden Sie den Widerstand (R) - Suchen Sie nach dem Wert des Widerstands in der Schaltung.Wenn es in Kilo-Ohm (Kω) angegeben ist, multiplizieren Sie es mit 1.000.Wenn es in Mega-Ohm (Mω) ist, multiplizieren Sie es mit 1.000.000.

• Finden Sie die Kapazität (c) - Überprüfen Sie den Wert des Kondensators.Wenn es in Mikrofarads (µF) ist, multiplizieren Sie sie mit 10⁶.Wenn es in Nanofarads (NF) ist, multiplizieren Sie mit 10⁹.Wenn es in Picofarads (PF) ist, multiplizieren Sie mit 10¹².

• Multiplizieren Sie R und C. - Sobald beide Werte in den richtigen Basiseinheiten (Ohm und Farads) sind, multiplizieren Sie sie miteinander.Das Ergebnis ist die Zeitkonstante TDas zeigt, wie schnell sich die Spannung über den Kondensator im Laufe der Zeit ändert.

Die Zeitkonstante liefert ein klares Bild davon, wie der Kondensator nach einer plötzlichen Änderung reagiert, wie ein Schalter.Nach einmal konstant (1T), der Kondensator greift herum 63,2% der Versorgungsspannung, wenn sie aufgeladen wird.Nach Fünf Zeitkonstanten (5T), es ist mehr als 99% berechnet .Zu diesem Zeitpunkt behandeln die meisten Schaltungen den Kondensator als „voll“ aufgeladen.Das gleiche Timing funktioniert umgekehrt, wenn der Kondensator entlädt - es fällt nach einer Zeitkonstante auf etwa 36,8% und entlädt sich nach fünf fast vollständig.Die Zeitkonstante ist nicht nur eine Zahl, sondern auch, wie sich Ihr Schaltkreis verhält.

Wenn Sie a bauen TiefpassfilterDie Zeitkonstante steuert, wie schnell der Filter auf Signaländerungen reagiert.In a TimerschaltungAnwesend T Bestimmt, wie lange es dauert, bis der Ausgang ausgelöst oder zurückgesetzt wird.In Schaltkreise verzögernEs wird festgelegt, wie lange das System wartet, bevor sie antworten.Wenn Sie wissen, wie Sie die Zeitkonstante berechnen und anwenden können, wird sichergestellt, dass Ihr Design genau im richtigen Moment reagiert, ob Sie etwas langsam einschalten, Geräusche herausfiltern oder eine Aktion verzögern können.

Entwerfen und Testen einer RC -Schaltung

Das Entwerfen einer RC -Schaltung beginnt mit einem klaren Ziel.Unabhängig davon, ob Sie einen Timer, einen Signalfilter oder einen Schaltkreis erstellen, der Wellenformen formt, ist Ihr erster Schritt immer der gleiche: Definieren Sie, was die Schaltung tun muss und wie er sich verhalten sollte.

Klären Sie die Funktion der Schaltung

Fragen Sie sich vor der Auswahl von Teilen, was die Schaltung erreichen soll.

• Für ZeitschaltungenSie werden sich darum kümmern, wie lange es dauert, bis die Spannung steigt oder fällt.

• Für FilterSie müssen steuern, wie die Schaltung auf verschiedene Frequenzen reagiert.

• Für WellenformformungSie möchten verwalten, wie Signale glätten oder schärfen.

Sobald dies klar ist, identifizieren Sie die erforderlichen Parameter, wie z. B. Eingangsspannung, den erwarteten Strombereich und wie schnell die Schaltung reagieren sollte.

Wählen Sie den richtigen Widerstand und den richtigen Kondensator

Das Verhalten eines RC -Schaltkreises wird durch seine Zeitkonstante definiert, geschrieben als:

T = R × c

Wo:

• R ist der Widerstand (in Ohm)

• C ist die Kapazität (in Faraden)

• T ist die Zeitkonstante (in Sekunden), die bestimmt, wie schnell sich die Spannung ändert

Um die Geschwindigkeit der Schaltung anzupassen:

• Verwenden Kleinere R- oder C -Werte Damit die Schaltung schneller reagieren lässt

• Verwenden größere R- oder C -Werte die Reaktion zu verlangsamen

Dieser Teil des Designs umfasst häufig Kompromisse.Die Reduzierung des Widerstands beschleunigt beispielsweise die Reaktionszeit, kann jedoch den Stromverbrauch erhöhen.

Simulieren Sie die Schaltung vor dem Bau

Bevor Komponenten auf ein Stirnboard gelegt werden, ist es eine gute Idee, das Design virtuell zu testen.Simulationstools helfen Ihnen, vorherzusagen, wie sich die Schaltung verhalten wird, ohne physische Teile zu benötigen.

Die beliebte Schaltungssimulationssoftware umfasst:

• Ltspice

• Proteus

• Multisim

Mit diesen Tools können Sie Spannungen und Strom im Laufe der Zeit anzeigen, die Frequenzantworten überprüfen und verschiedene R- und C -Kombinationen schnell ausprobieren.

Erstellen und testen Sie den Prototyp

Sobald die Simulation vielversprechend aussieht, bauen Sie die Schaltung auf einem Brotbrett.Auf diese Weise können Sie überprüfen, wie es sich unter tatsächlichen Bedingungen wie Temperaturänderungen, Komponentenverträglichkeiten und Stromversorgungsgeräuschen verhält.Während des Tests möchten Sie beobachten, wie der Kondensator berechnet und entlassen wird und ob dies der von Ihnen berechneten Zeitkonstante entspricht.

Leistung messen und analysieren

Verwenden Sie Messwerkzeuge (z. B. einen Oszilloskop oder einen Datenlogger), um die Spannung über die Zeit zu erfassen.Vergleichen Sie dies dann mit der erwarteten Antwort:

• Für Timing -AnwendungenKonzentrieren Sie sich darauf, wie lange es dauert, um bestimmte Spannungen während der Ladung oder Entladung zu erreichen.Dies geschieht normalerweise mit transienter Analyse.

• Für FilterschaltungenUntersuchen Sie, wie der Ausgang auf verschiedene Eingangsfrequenzen reagiert.Dies zeigt, ob der Frequenzgang mit Ihren Designzielen übereinstimmt.

Unterschiede zwischen RC-, RL- und RLC -Schaltungen

Bei der Gestaltung einer Schaltung ist es hilfreich, die Stärken und Rollen verschiedener Kombinationen von Grundkomponenten zu kennen.Drei übliche Typen sind RC-, RL- und RLC -Schaltungen.Jeder verhält sich unterschiedlich und passt zu bestimmten Arten von Aufgaben.

RC -Schaltungen

Ein RC -Schaltkreis kombiniert einen Widerstand und einen Kondensator.Diese Paarung wird in Situationen, in denen Sie steuern müssen, wie schnell die Spannungen steigen oder fallen müssen.

Sie finden häufig RC -Schaltungen in:

• Zeitschaltungen, wie Verzögerungs -Timer oder Pulsgeneratoren

• Signalfilter, besonders Tiefpass- oder Hochpassfilter

• Grundlegende Glättung oder Wellenformformung Anwendungen

Sie sind beliebt, weil sie leicht zu bauen, erschwinglich zu bauen und sehr wenig Platz einzunehmen.Wenn Ihr Ziel darin besteht, Signale zu verzögern, Geräusche herauszufiltern oder Spannungskurven zu formen, ohne sich über Resonanz oder hochfrequente Präzision zu sorgen, ist eine RC-Schaltung normalerweise die richtige Wahl.

RL -Schaltungen

Eine RL -Schaltung verwendet einen Widerstand und einen Induktor.Anstatt sich damit zu befassen, wie sich die Spannung im Laufe der Zeit ändert (wie in RC -Schaltungen), konzentrieren sich RL -Schaltungen stärker darauf, wie sich der Strom verhält, insbesondere in Systemen, in denen Magnetfelder wichtig sind.

Diese werden oft verwendet in:

• Stromversorgung Glättung

• Elektromotoren oder Transformatoren

• Systeme, die auf induktivem Lastverhalten beruhen

Induktoren widerstehen den Stromveränderungen, wodurch die RL -Schaltkreise zum Umgang mit plötzlichen Spitzen wirksam werden und die Systeme bei der Aufrechterhaltung des stetigen Stromflusses helfen.

RLC -Schaltungen

RLC -Schaltkreise kombinieren Widerstände, Induktoren und Kondensatoren zu einem einzigen System.Bei korrekter Einstellung können diese Schaltungen bei bestimmten Frequenzen Resonanz finden, was sie in Anwendungen nützlich macht, bei denen eine präzise Frequenzregelung erforderlich ist.

Normalerweise finden Sie RLC -Schaltungen in:

• Funkempfänger und Sender

• Signalabstimmung und Bandpassfilter

• Oszillatorschaltungen zur Erzeugung von Wellenformen

Obwohl sie komplexer sind als RC- oder RL-Schaltungen, macht ihre Fähigkeit, frequenzspezifische Signale zu verarbeiten, sie zur Auswahl für fortschrittlichere Elektronik.

Häufige Missverständnisse über Zeitkonstanten

Obwohl das Konzept einer Zeitkonstante (T) scheint einfach zu sein, es gibt einige weit verbreitete Missverständnisse, die zu Designfehlern oder falschen Annahmen führen können.Gehen wir durch einige der häufigsten und klären, was passiert.

Der Kondensator ist nach einer Zeitkonstante vollständig aufgeladen

Dies ist ein häufiges Missverständnis.Es ist leicht anzunehmen, dass der Kondensator nach einer Zeitkondensspannung 100% der Versorgungsspannung sein sollte.Aber so funktioniert exponentielles Ladung nicht.Nach einmaliger Zeit konstant (T), der Kondensator berechnet etwa 63,2% der Versorgungsspannung, nicht die volle Menge.Die Ladekurve beginnt steil, verlangsamt sich aber im Laufe der Zeit.Um der vollen Spannung (über 99%) sehr nahe zu kommen, benötigt die Schaltung etwa das Fünffache der Zeitkonstanten (5T).Während die anfängliche Änderung schnell ist, dauert der letzte Teil des Ladevorgangs länger.

Die Zeitkonstante ändert sich nie

Es mag so aussehen, als ob Sie berechnen, wenn Sie berechnen T, es ist repariert.Aber in tatsächlichen Schaltungen ist das nicht immer wahr.Die Zeitkonstante ist das Produkt des Widerstands (R) und der Kapazität (c), und beide Werte können aufgrund von Bedingungen wie Temperaturänderungen, Komponentenalterung oder Toleranzunterschieden zwischen Teilen verschoben werden.Zum Beispiel kann ein Widerstand bei Warm geringfügig zunehmen, oder das Verhalten eines Kondensators kann mit zunehmendem Alter driften.Diese Änderungen können beeinflussen, wie schnell der Schaltkreis reagiert, auch wenn alles andere gleich bleibt.

Zeitkonstanten sind nur in einfachen RC -Schaltungen wichtig

Weil T wird oft im Kontext grundlegender RC -Schaltungen eingeführt, es ist leicht zu glauben, dass es dort nur relevant ist.Aber das ist alles andere als die ganze Geschichte.In fortgeschritteneren Schaltungen wie mehrstufigen Filtern, Integratorketten oder Feedback-Steuerungssystemen können Sie mehrere Zeitkonstanten zusammenarbeiten.Jeder trägt zur Gesamtreaktion bei.Einige beeinflussen das System schnell, während andere das langsamere und langfristige Verhalten prägen.Zu verstehen, wie diese Zeitkonstanten interagieren, ist der Schlüssel zur feinsten Komplex-Schaltungsleistung.

Abschluss

Wenn Sie verstehen, wie RC -Schaltungen funktionieren und wie sich die Zeitkonstante auf ihr Verhalten auswirkt, wird leistungsstarke Werkzeuge für die Gestaltung reaktionsschneller, stabiler und effizienter elektronischer Systeme freigeschaltet.Unabhängig davon, ob Sie einen Verzögerungs-Timer, einen Tiefpassfilter oder einen Wellenform-Shaper erstellen, ermöglicht es Ihnen, die Beziehung zwischen Widerstand, Kapazität und Zeit zu beherrschen, die die Schaltungsreaktion genau steuern.Mit klaren Formeln, Beispielen und Entwurfsschritten entspricht dieser Leitfaden Sie, um intelligentere Entwurfsentscheidungen zu treffen und das Verhalten des Schaltkreises mit Zuversicht zu beheben.

Häufig gestellte Fragen [FAQ]

1. Was bedeutet die Zeitkonstante in einer RC -Schaltung?

In einer RC -Schaltung die Zeitkonstante, gekennzeichnet durch den griechischen Buchstaben Tau (T) stellt die Zeit dar, die die Spannung über den Kondensator benötigt, um während des Aufladens auf etwa 63,2% ihres Endwerts zu steigen oder während des Entladens auf etwa 36,8% zu fallen.Es ist ein Maß dafür, wie schnell der Kondensator auf eine Spannungsänderung reagiert, und spiegelt den kombinierten Effekt des Widerstandsverlangsamungsstromflusses und des Speicherlades des Kondensators wider.

2. Wie leitet man die Zeitkonstante eines RC -Schaltkreises ab?

Die Zeitkonstante wird durch Analyse des Spannung und des Stromverhaltens in einer RC-Schaltung der Serie RC unter Verwendung von Kirchhoffs Spannungsgesetz und der Ladungsspannungsbeziehung des Kondensators abgeleitet.Bei der Lösung der Differentialgleichung, die beschreibt, wie der Kondensator im Laufe der Zeit lädt oder entlädt, umfasst der exponentielle Term das Produkt des Widerstands (R) und die Kapazität (c).Dieses Produkt, RC, erscheint im Nenner des Exponenten und definiert die Rate, mit der die Schaltung auf eine Spannungsänderung reagiert.Daher die Zeitkonstante T ist gleich RC.

3. Wie lautet die Zeitantwort des RC -Schaltkreises?

Die zeitliche Reaktion eines RC -Schaltkreises beschreibt, wie sich die Spannung über den Kondensator nach einem plötzlichen Ereignis wie Anwenden oder Entfernen einer Stromquelle ändert.Beim Laden steigt die Spannung nach einer exponentiellen Kurve allmählich an und erreicht nach einer Zeitkonstante ungefähr 63,2% der Versorgungsspannung.Bei der Entlassung nimmt die Spannung exponentiell ab und sinkt nach einer Zeitkonstante auf etwa 36,8% ihres Anfangswertes.Diese reibungslose, nicht-instantane Änderung ist wichtig für Timing- und Filteranwendungen.

4. Warum ist 63,2 eine Zeit konstant?

Der Wert von 63,2% ergibt sich aus dem exponentiellen Verhalten der Ladekurve in einer RC -Schaltung.Nach einmaliger Zeit konstant (T) Der mathematische Ausdruck für die Spannung wird V (1 - E^–1) und E^–1 ist ungefähr 0,368.Subtrahieren von 1 ergibt 0,632 oder 63,2%, was der Prozentsatz der endgültigen Spannung ist, die nach einem erreicht ist T.Dies ist keine willkürliche Zahl, sondern das natürliche Ergebnis der exponentiellen Ladegleichung.

5. Warum ist Tau gleich RC?

Tau ist gleich RC, da Widerstand (R) steuert, wie schnell Strom in den Kondensator fließen kann, während die Kapazität (c) bestimmt, wie viel Ladung der Kondensator speichern kann.Wenn diese beiden Elemente zusammenarbeiten, setzen sie das Tempo für die Spannungsänderung des Kondensators.Die Lösung für die Lade- oder Entladungsgleichung des Schaltkreises zeigt, dass die Änderungsrate durch das Produkt von R und C bestimmt wird, was die Zeitkonstante der Schaltung definiert T.